ref:Thermal Modelling of GaN & InP RF Devices with Intrinsic Account for Nanoscale Transport Effects
IEDM invited的文章,基于第一性原理,用蒙特卡洛仿真观察到了三倍的hotspot temperature
- Monte Carlo simulator that solves the Boltzmann transport equation (BTE) governing the microscopic heat carriers [8] with first-principles phonon/electron dispersions and scattering rates
先用1D的MC确定了材料的热导率和界面热阻
这个图也有意思的,杂质加剧声子散射从而降低热导率
有趣的发现,于2DMC相比,均匀热源会低估峰值温度,而忽略BEOL又会提高峰值温度。文中指出,使用简化的均匀热源模型会得到完全错误的heat profile,但可以准确预测热点温度,这和之前那篇用拉曼光谱拟合的结论符合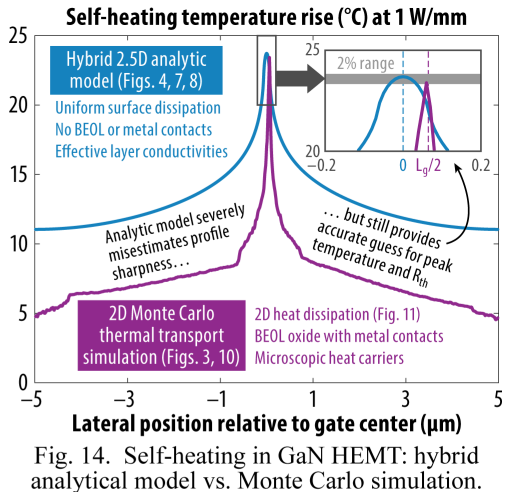
交流模拟对应阻抗,方法是先将热源设置成sin形式,得到热阻抗得到阶跃响应,然后对输入波形卷积得到温度曲线
ref:Self-Heating and Equivalent Channel Temperature in Short Gate Length GaN HEMTs
这篇文章提出了短沟道HEMT的等效温度(equivalent channel temperature)
同样使用Sentaurus device,产热考虑了recombination heat和Peltier heat
cutline在表面以下2.5nm,条件为Vg=0,Vd=10,这种分布也是老生常谈了,贴出来玩玩
等效沟道温度的定义是,与当前I-V相交的“等温分布曲线”
左图选取了等功率下改变gate电压的温度分布。为啥发热不守恒?
gate电压变小,peak温度升高。右图显示了peak温度-Vd的斜率受Vg影响,但它们的等效温升不受Vg影响,这代表了什么?
Id=Wqnv
二维电子气的密度几乎和温度无关(300-600k)6%
电子drift速度是一个分段函数,取决于有没有饱和
$$
v(E, T)= \begin{cases}\frac{\mu_0(T) E}{1+a E / E_C(T)}, & E<E_C(T) \ v_{\mathrm{sat}}(T), & E>E_C(T)\end{cases}
$$
不同等效温度下沟道中的场强,mobility,electron velocity分布
可以翻译为,高温主要限制沟道中的最大mobility,而GD的电场尖峰远超饱和的电场,所以热点的物理参数基本没有受影响
温度升高时,热点区域以外的沟道会有更高的阻值,也会有对应产生更多焦耳热
这不就巧了吗,热点外的沟道原理gate,因此不受Vg的影响
思路明晰但又有意思的文章
ref:Modeling Bias Dependence of Self-Heating in GaN HEMTs Using Two Heat Sources
如题,讲了一个双热源模型,我现在感觉仿真HEMT多半要靠gate热源模型惹。这篇紧接着上一篇的思路,将沟道与热点的产热分开算
这个双热源模型合理且聪明
- 首先用sentarus仿真发热
- 然后进行分段计算
- 划分区域后建模为双热源
3D模型就得简化热源啊(哭腔)
观察发现,HS2趋于水平,HS1开始发热都出现在Vsa附近,这也是符合物理图像的,据此提出一阶双热源模型
$$
\begin{cases}P_1=I_{\mathrm{d}} V_{\mathrm{d}}, \quad P_2=0, & \text { for } \quad V_{\mathrm{d}} \leq V_{\mathrm{dsat}} \ P_1=I_{\mathrm{d}} V_{\mathrm{dsat}}, \quad P_2=I_{\mathrm{d}}\left(V_{\mathrm{d}}-V_{\mathrm{dsat}}\right), & \text { for } \quad V_{\mathrm{d}}>V_{\mathrm{dsat}}\end{cases}
$$
接下来检验模型的有效性
- 文中的建模是有效的
- gate length从0.1um增大到0.8um时,采用0.16的gate热源依然有好的热仿真效果,这是因为gate热源来自电场集中
$$
T_{\max }=T_0+R_{\mathrm{sub}} P_{\mathrm{diss}}+R_1 P_1+R_2 P_2
$$
然后文章提出了一个计算Tmax的公式,乍一看有点脱了裤子放屁,但是用来快速迭代或许会很有用 - R1,R2分别是从HS1,HS2出发到substrate的热阻,这里的热阻包含了扩散热阻
- Pdissipate这一项的意思是,通过GaN层后,R1R2都扩散到finger大小
- 对于扩散热阻显著的低估了,文章也没有给出这么计算的有效性
首先来品鉴一篇2021年的IEDM ref:1.2 kV GaN/SiC-based Hybrid High ElectronMobility Transistor with Non-destructive Breakdown
这篇文章写于2021年,与目标文献的区别是
- SiC是lateral
- 没有实现indevice interconnect,将B和S分开


单独测试了SiC diode的电场分布,well 较厚的时候电场分布较均匀,HyFET不存在这个问题

大概明白了,这个器件的工作得靠探针的1Moh阻值。
-电压增加时,SiCdiode 因压控电阻减小
-GaN HEMT不被击穿
-和hyFET的原理完全不同,这个相当于用SiC diode做了个钳位电压,功劳主要是把4off axis和GaN substrate集成,但因为时lateral器件,也没有证明sic的质量,比起陈老师组的差远了感觉
下一篇yangshen新作ref:Two-temperature principle for evaluating electrothermal performance of GaN HEMTs感觉是之前那篇等效沟道温度加上了非傅里叶传热的续作
我产生了新的思路……
既然双热源模型基于夹断,那么在SiC中一定也存在类似的现象,这项工作的有趣性也就体现出来了,如果能够先用2D的仿真得到双热源模型,再integrated到封装里进行带封装的仿真,甚至dynamic的仿真,岂不美哉